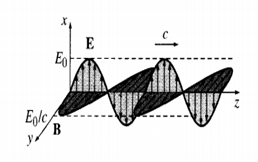
Wave-particle duality still remaining a mystery, we can say that we are always surrounded by energy in the forms of waves (mechanical or electromagnetic) and particles.  We always feel air blowing, see water flowing and light shining on us. When these all interact with a body, they always transfer energy or say momentum to the body and that is why we see things bending, blowing, flying when high speed winds and strong water waves or particles interact with the objects. The vibration of an electric charge generates the electromagnetic waves which are composed of both an electric and a magnetic field components perpendicular to each other as well as perpendicular to the direction wave propagation. In case of light (which also EM wave/radiation) particularly, the particle concept is taken over by wave when the base particle “photon” is said to have rest mass “zero”. 

So the transfer of momentum by the radiation takes place in terms of waves. EM radiation interference with a body is totally a different phenomenon to EM radiation mechanical interaction.  In case of mechanical interaction of EM radiation, the radiation will fall on the body and either will be reflected or absorbed by the body.  The interaction of EM radiation with an object will transfer energy or momentum to the body from the EM radiation. The transfer of momentum i.e. energy will give rise to a mechanical EM radiation pressure and our interest is to know how much pressure is being transferred to the body by EM radiation of different frequencies. Progressing towards the use of advanced generation (like 5G or 6G) communication systems has prompted for a serious discussion about the EM radiation pressure and its effects on living things in general and on human in particular in present days while recent occurrence of COVID-19 pandemic all over the world has further intensified the topic.

 

Energy and momentum in EM waves

The overall EM waves spectrum and for EM radiation in the visible range i.e. light is shown in Table 1a & b (Ref.1).  When an electromagnetic wave of any frequency (c=fλ) is scattered or absorbed by an object, the wave exerts a radiation pressure on the object [1,2]. The electromagnetic radiation pressure is the type of mechanical pressure exerted upon on the surface of any object due to the exchange of momentum between the object and the electromagnetic field.  The associated force due to radiation pressure is called the radiation pressure force, or sometimes just the force of light. In electrostatics and magnetostatics the Newton’s third law holds good, but not in electrodynamics and the proof of conservation of momentum rests on the cancellation of internal forces, which follows from the Newton’s third law. Tempering with the third law will always place conservation of momentum in jeopardy, and there is no principle in Physics more sacred than conservation of momentum. Therefore, momentum conservation is rescued in electrodynamics by the realization that the fields themselves carry momentum same as they carry energy with them. The momentum conservation in EM radiation is restored only by adding the EM radiation momentum to the mechanical momentum of the charges.

 

Table 1a (Ref. 1)

 

 

 

Table 1b (Ref. 1)

 

The energy per unit volume stored in EM fields is given as:

u=12?0E2+1μ0B2                                                 (1)

In case of a monochromatic (having single frequency or wavelength) plane wave

B2=1c2E2=μ0?0E2                                                  (2)

As the wave ravels, it carries energy or energy density of EM radiation/waves which is proportional to the square of the amplitude of the electric (or magnetic) field component and is given as u= ?0E2. The energy flux density (energy per unit area, per unit time) transported by the fields is given by the Poynting’s vector S=1μ0(EXB). EM fields not only carry energy, they also carry momentum and the momentum density stored in the fields is ℘=1c2S . The time average values of these quantities can be written as:  <u>= 12?0E2;    <S>=12c?0E02 ;     <℘>=12c?0E02

The average power per unit area transported by an EM wave is called the intensity:

I  ≡  <S>  =   12c?0E02                                                  (3)

As in the case of conservation of charge and conservation of energy, conservation of momentum can be given a differential formulation as ∂∂t℘mech+℘em=∇?T, where T is momentum flux density or electromagnetic stress (force per unit area) acting on the surface. Thus, when light falls on a perfect absorber it delivers its momentum to the surface.  In a time ?t the momentum transfer is  ?p=<℘>Ac?t. So the radiation is force/area, and force is change in momentum w.r.t. time. Hence EM radiation should exert a pressure on objects when it hits them.  Radiation pressure= F/A = (dp/dt)/A = [d(energy/speed)/dt]/A = [power/speed]/A = [power/area]/speed = I/c, where, I = power/area is called wave’s irradiance. If the radiation reflects, then the momentum is twice and so the radiation is also twice.

 

Radiation pressure applications

Concern about and understanding of EM radiation pressure in general and light as in particular have made it possible to use it in many exotic scientific and technological applications. Most natural light sources exert negligibly small forces on objects and this subtle effect was first demonstrated by the American physicists Ernest Fox Nichols and Gordon Hull in 1903. However, this radiation pressure can be more consequential in with high powered lasers or a number of astronomical settings. Worldly applications of EM radiation pressure became feasible with the arrival of lasers in the 1960s. Because of the small diameters of output laser beams  and their excellent focusing properties, laser intensities are generally orders of magnitude larger than the intensities of natural light sources. On the largest scale, the most powerful laser systems are being employed to compress and heat target materials in nuclear fusion inertial confinement schemes. Further, the light radiation forces from table-top laser systems are also being used to manipulate atoms and microscopic objects. The techniques of laser cooling and trapping, pioneered by the Physics Nobelists (1997) Steven Chu, William Phillips, and Claude Cohen-Tannoudji, slow a gas of atoms in an “optical molasses” of intersecting laser beams. Using the laser cooling techniques, temperatures below 10⁻⁶ K (one-millionth of a degree above absolute zero) have been achieved. In a recently developed “Optical tweezers” is a related technique in which a tightly focused laser beam exerts a radiation force large enough to deflect, guide, and trap micron-sized objects ranging from dielectric spheres to biological samples such as viruses, single living cells, and organelles within cells. Development of optical tweezers have been awarded Physics Nobel Prize in 2018 to Arthur Ashkin.

Effect of EM radiation

Growing need and dependence on the advanced technology for the increasing frequency range of wireless communication, people are more concerned about its harmful effects on human health.  People always quote references of some bad effects of high frequency EM radiations around them, however, without any scientific basis. The Table 2 gives the frequency range for different types of EM radiations which we generally encounter in our daily lives. It is very clear from Table 2 that the frequency of light radiation is much higher as compared to even the highest 6G mode of wireless communication. The radiation pressure of light from sun on earth is about 9.08 μPa (μN/m²) which is very-2 less. On similar lines, we can say that the EM radiation pressure from other sources like radio, TV and communication devices working with 4G, 5G or higher generation will also be very less which will not impact human life (Ref.3) Power density of EM radiation as a function of its frequency and exposure time is an important parameter to evaluate the health effects of EM radiation pressure. Table 3 (Ref. 4) gives a brief look about power density as a function of EM radiation frequency and exposure time. It becomes very clear that even with low power density of advanced generation communication systems, the power density or radiation pressure being exerted on the user will definitely depend on its frequency and exposure time.  Therefore, to minimise the harmful effects of EM radiation pressure, it will always be beneficial to control the exposure time to the communication devices or sources using advanced generation communication system. 

 

Table 2

Sl No.	Mode of EM radiations		Frequency range
	Light		405–790 THz
	Radio & TV		3kHz-300GHz
	Phone/Mobile generation	1G	150-900MHz
		2G	900MHz-1.8GHz
		3G	1.6-2.0GHz
		4G	2.0-8.0GHz
		5G	3.0-300GHz
		6G	>95GHz (750-1100GHz)

 

Table 3 (Ref. 4)

 

References

1. Introduction to Electrodynamics by David J Griffiths, Prentice-Hall of India Private Limited, New Delhi (1999), Chapter-9: 9.2.3-Energy and momentum of Electromagnetic waves, pp.380.
2. Classical Electrodynamics (3^rd Edition) by J.D. Jackson, John Wiley & Sons Inc. (USA) (1999), Chapter-6:6.6-Poynting’s theorem and conservation of energy and momentum for a system of charged particles and electromagnetic fields, pp.258.
3. S. Wall et al, Real-world cell phone radiofrequency electromagnetic field exposures, Environmental Research 171 (2019) 581–592.
4. C. Törnevik et al., Time Averaged Power Control of a 4G or a 5G Radio Base Station for RF EMF Compliance, in IEEE Access, vol. 8, pp. 211937-211950, 2020, doi: 10.1109/ACCESS.2020.3039365.